Rhythm class#

This class is used for making/working with rhythms in the musical sense.

class thebeat.music.Rhythm(iois, time_signature=(4, 4), beat_ms=500, is_played=None, name=None)[source]#

The Rhythm class can be used for working sequences that are rhythmical in the musical sense. This means that in addition to having inter-onset intervals (IOIs) that represent the timing of the events in the sequence, Rhythm objects have musical properties such as a time signature, a beat duration, and they may contain rests.

The Rhythm class is also used as the basis for a Melody.

For more info on these properties, please refer to the class’s __init__().

__init__(iois, time_signature=(4, 4), beat_ms=500, is_played=None, name=None)[source]#

Constructs a Rhythm object.

Parameters

iois – An iterable of inter-onset intervals (IOIs). For instance: [500, 500, 400, 200].
time_signature (default: (4, 4)) – A musical time signature, for instance: (4, 4). As a reminder: the upper number indicates how many beats there are in a bar. The lower number indicates the denominator of the value that indicates one beat. So, in (4, 8) time, a bar would be filled if we have four \(\frac{1}{8}\) th notes.
beat_ms (default: 500) – The value (in milliseconds) for the beat, i.e. the duration of a \(\frac{1}{4}\) th note if the lower number in the time signature is 4.
is_played (default: None) – A list or array containing booleans indicating whether a note should be played or not. Defaults to [True, True, True, ...].
name (default: None) – Optionally, you can give the Sequence object a name. This is used when printing, plotting, or writing the Sequence object. It can always be retrieved and changed via Rhythm.name.

Examples

>>> iois = [500, 250, 250, 500, 500]
>>> r = Rhythm(iois)
>>> print(r.onsets)
[   0.  500.  750. 1000. 1500.]

>>> iois = [500, 250, 250, 500]
>>> r = Rhythm(iois=iois, time_signature=(3, 4), beat_ms=250)
>>> print(r.note_values)
[2 4 4 2]

copy(deep=False)#

Returns a copy of itself. See copy.copy() for more information.

Parameters: deep (bool, default: False) – If True, a deep copy is returned. If False, a shallow copy is returned.

property duration: numpy.float64#: Property that returns the summed total of the inter-onset intervals.

property fractions: numpy.ndarray#

Calculate how to describe the rhythm in fractions from the total duration of the sequence.

Example

A sequence of IOIs [250, 500, 1000, 250] has a total duration of 2000 ms. This can be described using the fractions \(\frac{1}{8}, \frac{2}{8}, \frac{4}{8}, \frac{1}{8}\), so this method returns the fractions [1/8, 2/8, 4/8, 1/8].

Examples

>>> r = Rhythm([250, 500, 1000, 250])
>>> print(r.fractions)
[Fraction(1, 8) Fraction(1, 4) Fraction(1, 2) Fraction(1, 8)]

classmethod from_fractions(fractions, time_signature=(4, 4), beat_ms=500, is_played=None, name=None)[source]#

This class method can be used for creating a Rhythm on the basis of fractions. The fractions can be input either as floats (e.g. 0.25) or as fractions.Fraction objects.

Parameters

fractions – Contains the fractions of the rhythm. For instance: [1, 2, 4].
time_signature (default: (4, 4)) – The time signature of the rhythm. For instance: (4, 4).
beat_ms (default: 500) – The duration of a beat in milliseconds. This refers to the duration of the denominator of the time signature.
is_played (default: None) – A list of booleans indicating which notes are played. If None, all notes are played.
name (default: None) – A name for the rhythm.

Example

The fractions represent for each note the proportion of the bar that the note takes up, taking into account the time signature. A few examples:

In 4/4 time, a quarter note would be 1/4, an eighth note 1/8, etc. In 4/8 time, a quarter note would be 1/2, an eighth note 1/4, etc.

In 5/4 time, we would input a quarter note as 1/5, an eighth note as 1/10, etc. In 5/8 time, we would input a dotted quarter note as 3/5, an eighth note as 1/5, etc.

Examples

>>> r = Rhythm.from_fractions([1/4, 1/4, 1/4, 1/4], time_signature=(4, 4), beat_ms=500)

>>> import fractions
>>> dotted_halfnote = fractions.Fraction(3, 5)
>>> halfnote = fractions.Fraction(2, 5)
>>> r = Rhythm.from_fractions([dotted_halfnote, halfnote], time_signature=(5, 4), beat_ms=500)

>>> r = Rhythm.from_fractions([1/4, 1/4, 1/4, 1/4], time_signature=(4, 8), beat_ms=500)

classmethod from_integer_ratios(numerators, time_signature=(4, 4), beat_ms=500, is_played=None, name=None)[source]#

Very simple conveniance class method that constructs a Rhythm object by calculating the inter-onset intervals (IOIs) as numerators * beat_ms.

Parameters

numerators – Contains the numerators of the integer ratios. For instance: [1, 2, 4].
time_signature (default: (4, 4)) – A musical time signature, for instance: (4, 4). As a reminder: the upper number indicates how many beats there are in a bar. The lower number indicates the denominator of the value that indicates one beat. So, in (4, 8) time, a bar would be filled if we have four \(\frac{1}{8}\) th notes.
beat_ms (default: 500) – The value (in milliseconds) for the beat, i.e. the duration of a \(\frac{1}{4}\) th note if the lower number in the time signature is 4.
is_played (default: None) – A list or array containing booleans indicating whether a note should be played or not. Defaults to [True, True, True, ...].
name (default: None) – Optionally, you can give the Sequence object a name. This is used when printing, plotting, or writing the Sequence object. It can always be retrieved and changed via Rhythm.name.

classmethod from_note_values(note_values, time_signature=(4, 4), beat_ms=500, is_played=None, name=None)[source]#

Create a Rhythm object on the basis of note values (i.e. note durations).

Note values are input as the denominators of the fraction. A note value of 2 means a half note, a note value of 4 means a quarternote etc. A triplet would be [12, 12, 12].

Parameters

note_values – A list or array containing the denominators of the note values. A note value of 2 means a half note, a note value of 4 means a quarternote etc. A triplet would be [12, 12, 12].
time_signature (default: (4, 4)) – A musical time signature, for instance: (4, 4). As a reminder: the upper number indicates how many beats there are in a bar. The lower number indicates the denominator of the value that indicates one beat. So, in (4, 8) time, a bar would be filled if we have four \(\frac{1}{8}\) th notes.
beat_ms (default: 500) – The value (in milliseconds) for the beat, i.e. the duration of a \(\frac{1}{4}\) th note if the lower number in the time signature is 4.
is_played (default: None) – A list or array containing booleans indicating whether a note should be played or not. Defaults to [True, True, True, ...].
name (default: None) – Optionally, you can give the Sequence object a name. This is used when printing, plotting, or writing the Sequence object. It can always be retrieved and changed via Rhythm.name.

Examples

>>> r = Rhythm.from_note_values([16, 16, 16, 16, 4, 4, 4], beat_ms=500)
>>> print(r.iois)
[125. 125. 125. 125. 500. 500. 500.]

classmethod generate_isochronous(n_bars=1, time_signature=(4, 4), beat_ms=500, is_played=None, name=None)[source]#

Simply generates an isochronous (i.e. with equidistant inter-onset intervals) rhythm. Will have the bars filled with intervals of beat_ms.

Parameters

n_bars (default: 1) – The desired number of musical bars.
time_signature (default: (4, 4)) – A musical time signature, for instance: (4, 4). As a reminder: the upper number indicates how many beats there are in a bar. The lower number indicates the denominator of the value that indicates one beat. So, in (4, 8) time, a bar would be filled if we have four \(\frac{1}{8}\) th notes.
beat_ms (default: 500) – The value (in milliseconds) for the beat, i.e. the duration of a \(\frac{1}{4}\) th note if the lower number in the time signature is 4.
is_played (default: None) – A list or array containing booleans indicating whether a note should be played or not. Defaults to [True, True, True, ...].
name (default: None) – If desired, one can give a rhythm a name. This is for instance used when printing the rhythm, or when plotting the rhythm. It can always be retrieved and changed via Rhythm.name.

classmethod generate_random_rhythm(n_bars=1, beat_ms=500, time_signature=(4, 4), allowed_note_values=None, n_rests=0, rng=None, name=None)[source]#

This function generates a random rhythmic sequence on the basis of the provided parameters.

It does so by first generating all possible combinations of note values that amount to one bar based on the allowed_note_values parameter, and then selecting (with replacement) n_bars combinations out of the possibilities.

Parameters

n_bars (default: 1) – The desired number of musical bars.
beat_ms (default: 500) – The value (in milliseconds) for the beat, i.e. the duration of a \(\frac{1}{4}\) th note if the lower number in the time signature is 4.
time_signature (default: (4, 4)) – A musical time signature, for instance: (4, 4). As a reminder: the upper number indicates how many beats there are in a bar. The lower number indicates the denominator of the value that indicates one beat. So, in (4, 8) time, a bar would be filled if we have four \(\frac{1}{8}\) th notes.
allowed_note_values (default: None) – A list or array containing the denominators of the allowed note values. A note value of 2 means a half note, a note value of 4 means a quarternote etc. Defaults to [4, 8, 16].
n_rests (default: 0) – If desired, one can provide a number of rests to be inserted at random locations. These are placed after the random selection of note values.
rng (default: None) – A numpy.random.Generator object. If not supplied numpy.random.default_rng() is used.
name (default: None) – If desired, one can give a rhythm a name. This is for instance used when printing the rhythm, or when plotting the rhythm. It can always be retrieved and changed via Rhythm.name.

Examples

>>> import numpy as np  # not required, here for reproducability
>>> generator = np.random.default_rng(seed=321)  # not required, for reproducability
>>> r = Rhythm.generate_random_rhythm(rng=generator)
>>> print(r.iois)
[125. 250. 125. 125. 500. 125. 125. 125. 500.]

>>> import numpy as np  # not required, here for reproducability
>>> generator = np.random.default_rng(seed=321)  # not required, here for reproducability
>>> r = Rhythm.generate_random_rhythm(beat_ms=1000,allowed_note_values=[2, 4, 8],rng=generator)
>>> print(r.iois)
[ 500. 1000.  500.  500. 1000.  500.]

property integer_ratios: numpy.ndarray#

Calculate how to describe the rhythm in integer ratio numerators from the total duration of the sequence by finding the least common multiplier.

Example

A sequence of IOIs [250, 500, 1000, 250] has a total duration of 2000 ms. This can be described using the least common multiplier as \(\frac{1}{8}, \frac{2}{8}, \frac{4}{8}, \frac{1}{8}\), so this method returns the numerators [1, 2, 4, 1].

Notes

The method for calculating the integer ratios is based on Jacoby and McDermott [JM17].

Caution

This function uses rounding to find the nearest integer ratio.

Examples

>>> r = Rhythm([250, 500, 1000, 250])
>>> print(r.integer_ratios)
[1 2 4 1]

property iois: numpy.ndarray#

The inter-onset intervals (IOIs) of the Sequence object. These are the intervals in milliseconds between the onset of an event, and the onset of the next event. This is the most important attribute of the Sequence class and is used throughout.

This getter returns a copy of the IOIs instead of the actual attribute.

property mean_ioi: numpy.float64#: The average inter-onset interval (IOI).

property note_values#

This property returns the denominators of the note values in this sequence, calculated from the inter-onset intervals (IOIs). A note value of 2 means a half note. A note value of 4 means a quarternote, etc. One triplet of three notes would be [12, 12, 12].

Caution

Please note that this function is basic (e.g. there is no support for dotted notes etc.). That’s beyond the scope of this package.

Examples

>>> r = Rhythm([500, 1000, 250, 250], time_signature=(4, 4), beat_ms=500)  
>>> print(r.note_values)  
[4 2 8 8]

>>> r = Rhythm([166.66666667, 166.66666667, 166.66666667, 500, 500, 500], beat_ms=500]  
>>> print(r.note_values)  
[12 12 12  4  4  4]

property onsets: numpy.ndarray#: Returns the event onsets (t values) on the basis of the sequence objects’ inter-onset intervals (IOIs).

plot_rhythm(filepath=None, staff_type='rhythm', print_staff=True, title=None, suppress_display=False, dpi=600, ax=None)[source]#

Make a plot containing the musical notation of the rhythm. This function requires you to install:

abjad (install via pip install abjad).
lilypond

For lilypond on Windows, make sure to follow the website’s instructions on how to make lilypond available to be run through the command line. Linux and Mac OS users are advised to either apt install lilypond or brew install lilypond. On Mac that requires you to install Homebrew.

The plot is returned as a matplotlib.figure.Figure and matplotlib.axes.Axes object, which you can manipulate.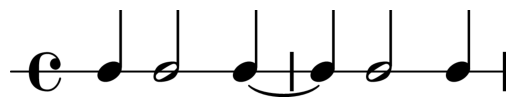

../../_images/plot_rhythm_rhythmstaff.png — A plot with the default `print_staff=True` and the default `staff_type="rhythm"`.#

../../_images/plot_rhythm_withstaff.png — A plot with the default `print_staff=True` and `staff_type="percussion"`.#

../../_images/plot_rhythm_nostaff.png — A plot with `print_staff=False`.#

Parameters

filepath (Union[PathLike, str, None], default: None) – Optionally, you can save the plot to a file. Supported file formats are only ‘.png’ and ‘.pdf’. The desired file format will be selected based on what the filepath ends with.
staff_type (str, default: 'rhythm') – Either ‘percussion’ or ‘rhythm’. ‘Rhythm’ is a single line (like a woodblock score). Percussion is drum notation.
print_staff (bool, default: True) – If desired, you can choose to print a musical staff (the default is not to do this). The staff will be a percussion staff.
title (Optional[str], default: None) – A title for the plot. Note that this is not considered when saving the plot as an .eps file.
suppress_display (bool, default: False) – If desired,you can choose to suppress displaying the plot in your IDE. This means that matplotlib.pyplot.show() is not called. This is useful when you just want to save the plot or use the returned matplotlib.figure.Figure and matplotlib.axes.Axes objects.
dpi (int, default: 600) – The resolution of the plot in dots per inch.
ax (Optional[Axes], default: None) – Optionally, you can provide an existing matplotlib.axes.Axes object to plot the rhythm on.

Return type

tuple[Figure, Axes]

Examples

>>> r = Rhythm([500, 250, 1000, 250], beat_ms=500)
>>> r.plot_rhythm()  

>>> r = Rhythm([250, 250, 500, 500, 1500], time_signature=(3, 4))
>>> fig, ax = r.plot_rhythm(print_staff=True, suppress_display=True)  
>>> plt.show()  

>>> r = Rhythm.from_note_values([4, 4, 4, 4])
>>> r.plot_rhythm(filepath='isochronous_rhythm.pdf')  

to_sequence()[source]#

Convert the rhythm to a Sequence object.

Return type: Sequence